瞬時にウソを見抜く「数学脳」の鍛え方
構成:村上 敬
編集:プレジデント社
数字は意図的に見せ方を変えられる危険性がある
 |
東北学院大学工学部教授 神永 正博氏(かみなが・まさひろ) 博士(理学)、東北学院大学工学部教授。大阪大学にて理学博士号を習得。過去にはエンジニアとして日立製作所で勤務した経験も。専門は、暗号理論(ICカード、ICタグなどの暗号解読、ハッキング防衛技術の開発)、作用素論、数理物理学。数字の本質を正しく見抜くための数学的思考法を記した『直感を裏切る数学』(講談社)や『ウソを見破る統計学』(講談社)など著書多数。 |
~切り取り方で数字は見かけを変えられる
さっそくですが、次の表(図表①) を見てください。
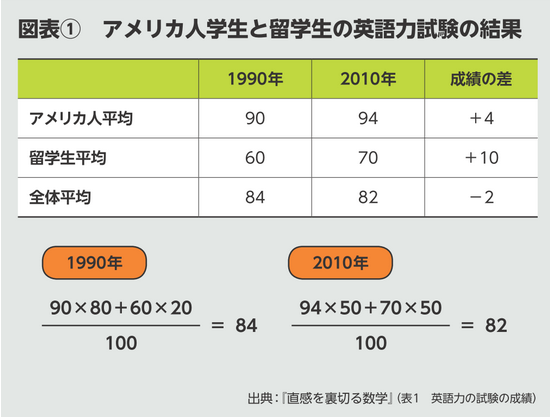
アメリカのある大学で、アメリカ人学生と留学生に英語力のテストをして、それぞれの平均点を示した架空の表です。1990(平成2)年はアメリカ人が90点で、留学生が60点。2010(平成22)年に同様のテストをしたところ、アメリカ人は94点、留学生が70点でした。20年間で、アメリカ人は4点、留学生は10点上がっています。
両方の平均点が上がっているのだから、当然、全体の平均点も上がっているように感じますよね。ところが、全体の平均点を計算すると、90年が84点であるのに対して10年は82点で、逆に2点下がっています。どうしてこんなことが起きると思いますか?
それは、アメリカ人と留学生の人数比が変わったからです。90年は学生100人のうちアメリカ人が80人、留学生が20人でしたが、10年はアメリカ人50人、留学生50人に。成績の良くないグループ(この場合は留学生)が増えたために、全体の平均点が下がったのです。このように「集団全体の性質と、集団を分けたときの性質が異なる」現象は、“シンプソンのバラドックス”と呼ばれています。もともと連続的に変化をしているデータでも、表の形で区切ると情報が失われて、この現象が起きるケースがあります。
厄介なのは、区切り方によってパラドックスを意図的に作り出せる点でしょう。例えば、平均年収の変化を示すとします。全体の年収は減っているのに、年収別階層の区切り方を工夫すれば、「どの階層でも年収が増えている」と主張することができます(図表②参照)。
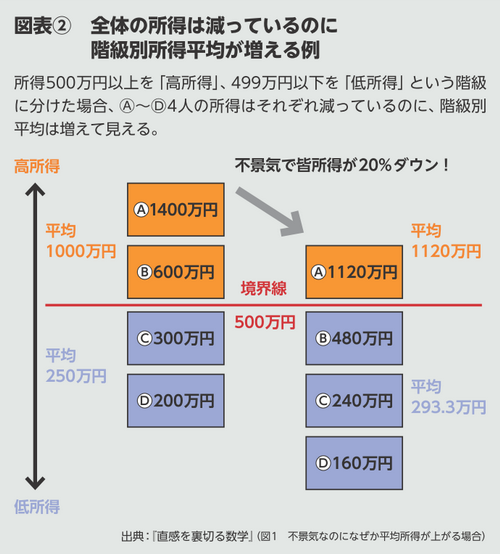
このように、誰かに「データに裏付けられている」と言われても、そのまま信じるのは危険です。数字はいくらでも見かけを変えられることを肝に銘じておいてください。
~「年収2000万円だと婚姻率100%」は本当?
見かけの数字に要注意という例をもう一つ挙げましょう。年収と婚姻率の関係を調べたとき、「年収2000万円以上は婚姻率100%」という結果になったとします。これだけ見ると、「年収が2000万円を超えれば絶対に結婚できる」ということになります。
ただ、その調査で年収2000万円以上だった人が一人だったらどうでしょう。たまたまその人が結婚していれば婚姻率は100%で、未婚なら0%。サンプルサイズが小さくて結果に偏りが出るため、何の参考にもなりませんね。
それくらいすぐに気づく、自分はそう簡単に騙されないぞと考えている人は多いでしょう。しかし、こうした偏りにまどわされる人は少なくありません。
私は東北学院大学で教鞭をとっていますが、同僚の工学部の先生から「工学部の女子学生は真面目で優秀」と聞くことがあります。しかし、これは間違い。成績や出席日数などを何年もの長期的に比べると、女子学生も男子学生もほぼ同じです。
ただ、工学部のわが学科には110人の定員中、1ケタしか女子学生がいません。そのため偏りが出やすく、単年で見ると「優秀な女子学生が多かった」という年があります。本当は同じくらい「不真面目な女子学生が多かった」という年もあるのですが、先入観があるのか、良いときのほうだけの印象で語ってしまうのです。
工学部の先生ですから、みなさん数字を扱うのは得意です。サンプルサイズが小さいと偏りが出ることも知っています。にもかかわらず、日常生活の中でこのような場面に出くわすと、実態を誤解して捉えてしまう。専門家でさえ騙されるのが、数字の怖さです。
数字やデータを見るときに注目すべきは「比率」と「絶対数」
~数学的思考があれば数字に動揺しなくなる
専門家でも予測が難しいことは、コロナの分析でもあらわになりました。昨年(2020年)5月、私も緊急事態宣言で時間ができたので、趣味と実益を兼ねて感染者数の分析をしてみました。東京都のデータをSEIRという数理モデルに当てはめて、その後の感染者数を予測。その結果、死者数40万人という数字が出てきました。いまならこの予測が正しくなかったことがわかりますね。
なぜそんな数字になったのか。それは感染確認数の初期のデータしかなかったからです。いま同じモデルを使って計算すれば、おそらくまったく違う結果になります。そういう意味で、数理モデルへの当てはめも後知恵に過ぎません。いくら分析のスキルがあっても、本当のことはすべてが終わらないとわからないのです。
ならば数学的思考なんて役に立たないではないかと考える人もいるでしょう。しかし、大切なのは、わからないということをわかること。数学的思考を身につければ、「いま見えているものがすべてではない」というある種の達観ができて、数字を見て動揺することがなくなります。例えば先ほどのコロナの分析でも、「これは大変」と警戒する一方で、「間違っているかも」と冷静に受け止められるようになります。
実はこうしたものの見方は、数学を勉強しなければ身につかない類いのものではありません。先ほどの工学部の女子学生の話も、文系の先生のほうがこの仕組みを理解していたりします。歴史学の先生は、「歴史は勝者によって書かれること」をご存じなので、数字も誰かに都合のいいように記述されうることがわかっているのでしょう。
そう考えると、数学的思考を身につけるために、必ずしも学校の教科書を開く必要はありません(一定の効果はあると思いますが)。もし学ぶとしたら、もっと基礎のところ―具体的には、比率と絶対数を理解することが大切です。英語の平均点や工学部女子学生の例も、サンプルの数(人数)に着目していれば、見かけや先入観に引っ張られにくくなります。難しい数理モデルを学ぶより、そのほうがずっと騙されにくくなるでしょう。
同テーマの記事はこちら
○ 賢い人ほどとらわれる10の思い込み:関 美和
○ ガセに踊らされず正しい“ネタ”を掴む!:高橋直子
